前言

上一节中，我们学习了偏序、格、格上的函数单调性和不动点定理等数学知识，留下了关于迭代算法的三个问题没有解答：

  1. 这个算法能够保证一定能终止（到达不动点/有解）吗？
  2. 如果上一个问题的答案是肯定的，那么只有一个解/不动点吗？如果有多个不动点，哪一个是最好的、或者说最精确的？
  3. 什么时候这个算法能够到达不动点呢？

本节，我们将陆续来回答这三个问题，并学习一种新的数据流分析应用——常量传播，以及一种基于迭代算法但做了改进的Worklist算法。另外，本节课将引出第二个实验作业——常量传播与Worklist求解器。

将迭代算法关联到不动点定理

首先，我们要将迭代算法与不动点定理关联起来，这样才能够利用不动点定理来解答上述问题。再来看一下不动点定理：

给定一个完全格$(L, \preccurlyeq)$，如果$f: L \rightarrow L$是单调的且$L$是有限的，那么：

  1. $f$的最小不动点可以通过以下方式得到：不断迭代计算$f(\bot)), f(f(\bot)),\ …\ , f^{k}(\bot))$，直到到达一个不动点。
  2. $f$的最大不动点可以通过类似的方式得到：不断迭代计算$f(\top)), f(f(\top)),\ …\ , f^{k}(\top))$，直到到达一个不动点。

在上一节课的开头，我们学习了这样一种观点——may&forward analysis算法可以视作不断输出一系列的k-tuple，直到某个k-tuple与上一个k-tuple相同：

$$ \text{iter 0}: (\bot, \bot,\ …\ , \bot) $$

$$ \text{iter i}: (v_{1}^{i}, v_{2}^{i},\ …\ , v_{k}^{i}) = X_{i} = F(X_{i-1}) $$

$$ \text{iter i+1}:(v_{1}^{i+1}, v_{2}^{i+1},\ …\ , v_{k}^{i+1}) = X_{i+1} = F(X_{i}) = X_{i} $$

上一节中，我们已经知道CFG上每个节点的OUT都对应一个完全（有限）格$L$，整个CFG上所有节点的OUT就构成了一个乘积格。对于乘积格$L^{k}$来说，如果构成它的每个格都是完全（且有限）格，那么$L^{k}$也是完全（且有限）格。至此，迭代算法满足不动点定理的第二个条件（格的有限性）。

接下来，我们需要证明迭代算法对应的函数$F$是单调的。根据之前的知识，$F$由两部分组成：

  1. transfer function $f$。
  2. join/meet function $\lfloor\rfloor/\lceil\rceil: L \times\ …\ \times L \rightarrow L$（控制流汇聚）。

根据之前的知识，Gen/Kill总是单调的，因此transfer function $f$是单调的。现在来证明一下join/meet function也是单调的，以join为例：$\forall\ x, y, z \in L, x \preccurlyeq y$，证明$x \lfloor\rfloor z \preccurlyeq y \lfloor\rfloor z$。

  1. 由$\lfloor\rfloor$的定义（最小上界）可知，$y \preccurlyeq y \lfloor\rfloor z$。
  2. 根据$\preccurlyeq$的传递性可知，$x \preccurlyeq y \lfloor\rfloor z$。
  3. 因此，$y \lfloor\rfloor z$是$x$的上界，也是$z$的上界。
  4. 而$x \lfloor\rfloor z$是$x$和$z$的最小上界，因此$x \lfloor\rfloor z \preccurlyeq y\lfloor\rfloor z$。

于是，我们证明了join function也是单调的，故不动点定理适用于前述迭代算法。

因此，根据不动点定理，前述迭代算法一定能达到不动点（问题1），且一定能够到达最小（最大）不动点（问题2）。

第三个问题实际上是问在最坏情况下，需要经过多少次迭代才能达到不动点。我们假设每次迭代只在一个节点OUT对应的格上走了一步，而格的高度是$h$（在格上从top到bottom的最长路径），CFG有$k$个节点，那么最多需要$i = h*k$次迭代才能达到不动点。至此，三个问题回答完毕。

格视角下的May/Must分析

接下来，李樾老师探讨了如何从格理论的视角来看待may和must分析。

假设下面这个幂集表示CFG中各节点的OUT对应的格，图中最上方是$\top$，最下方是$\bot$：

graph TD A("T {a, b, c}") --> B("{a, b}") A --> C("{a, c}") A --> D("{b, c}") B --> E("{a}") C --> E D --> E B --> F("{b}") C --> F D --> F B --> G("{c}") C --> G D --> G E --> H("⊥ { }") F --> H G --> H style A fill:#b12318 style H fill:#1d8daa

相应地，下图中左右两个竖立的椭圆分别代表在must分析和may分析中CFG各节点OUT组成的乘积格的结果：

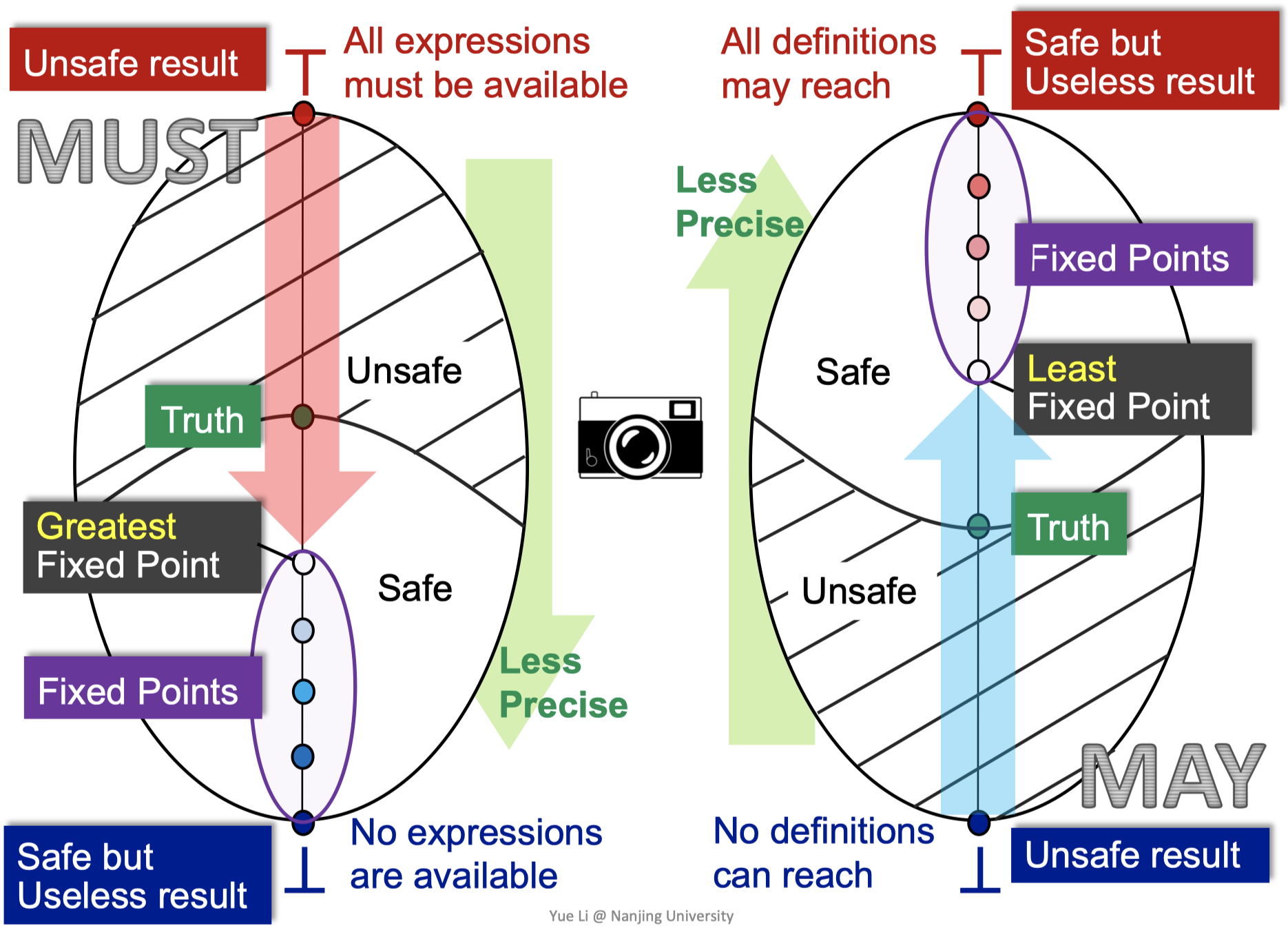
image-20230316155147853

无论是must还是may分析，都是从unsafe result向safe result方向移动，“从准往不准走”。其中must分析在这个乘积格上来看就是不断从$\top$往下走，越过truth（第一节课中讨论过sound、truth和complete的关系），我们的迭代算法会达到最大不动点；相反，may分析就是不断从$\bot$往上走，越过truth，我们的迭代算法会达到最小不动点。

为什么不动点一定在safe区域呢？这和迭代算法中的safe approximation有关，是需要设计来保证的。

这部分内容有点抽象，后面如果要用到相关知识，还是回过头来再听一下李樾老师的课程视频吧。

MOP和分配性（Distributivity）

接下来研究一下分析精度：我们得出的解的精度如何呢？这里介绍一下另一种解法：Meet-Over-All-Paths（MOP）。

我们定义$P$为从Entry到某个语句$S_{i}$的某一条路径（可能还会有别的路径），转换函数$F_{P}$是从Entry到$S_{i}$经过的所有的转换函数（$f_{S_{1}},\ …\ , f_{S_{i-1}}$）构成的复合转换函数，那么有：

$$ MOP[S_{i}] = \lfloor\rfloor / \lceil\rceil \ F_{P}(OUT[Entry]) $$

换言之，MOP在每条路径末尾计算数据流的值，然后将它们join/meet起来，寻找它们的lub/glb。

然而，有些路径可能是假的，例如，某些代码分支在动态运行时是永远不会执行到的。因此，MOP可能是不精确的。另外，MOP可能是无法终止的（unbounded），如遇到循环的情况；还可能是不可枚举的（not enumerable）。

那么，迭代算法求出的解和MOP求出的解的关系是什么呢？我们结合下面这个例子来说明：

graph LR A("Entry") --> B("S1") A --> C("S2") B --> E("S3") C --> E E --> F("Exit")

针对这个例子，我们有：

$$ IN[S_{4}] = f_{S_{3}}(f_{S_{1}}(OUT[Entry])\ \lfloor\rfloor\ f_{S_{2}}(OUT[Entry])) $$

$$ MOP[S_{4}] = f_{S_{3}}(f_{S_{1}}(OUT[Entry]))\ \lfloor\rfloor\ f_{S_{3}}(f_{S_{2}}(OUT[Entry])) $$

抽象一下，我们可以得到：

$$ Ours = F(x \lfloor\rfloor y) $$

$$ MOP = F(x) \lfloor\rfloor F(y) $$

很好理解，迭代算法会在过程中做join/meet操作，而MOP则是在路径最后才做join/meet操作。

在此基础上，我们来讨论一下迭代算法结果和MOP结果的关系：

  • 根据$\lfloor\rfloor$（最小上界）的定义可知，$x \preccurlyeq x \lfloor\rfloor y$且$y \preccurlyeq x \lfloor\rfloor y$，
  • 转换函数$F$是单调的，因此有$F(x) \preccurlyeq F(x \lfloor\rfloor y)$及$F(y) \preccurlyeq F(x \lfloor\rfloor y)$，
  • 故$F(x \lfloor\rfloor y)$是$F(x)$和$F(y)$的上界，而$F(x) \lfloor\rfloor F(y)$又是$F(x)$和$F(y)$的最小上界，
  • 因此可得$F(x) \lfloor\rfloor F(y) \preccurlyeq F(x \lfloor\rfloor y)$，即$MOP \preccurlyeq Ours$。

也就是说，我们的迭代算法的“精确度”通常要小于等于MOP。当转换函数$F$具有分配性（distributive）时，$MOP = Ours$，两者精确度才相同。事实上，我们在学习迭代算法时遇到的bit vector也好，gen/kill也好，集合交并集操作也好，都是distributive的。

然而，有一些数据流分析应用是not distributive的，比如下面这个常量传播分析。

常量传播（Constant Propagation）

老规矩，首先来看定义：

Given a variable x at program point p, determine whether x is guaranteed to hold a constant value at p.

根据该定义，我们可以确定的是CFG中每个节点的OUT应该是一个由$(x, v)$对组成的集合，其中$x$是变量，$v$是在该节点后$x$的值。

上一节中，我们定义一个基于格的数据流分析框架$(D, L, F)$：其中$D$指的是数据流的方向，包括前向和后向；$L$指的是由值域$V$和一个meet或join操作符构成的格；$F$指的是从$V$到$V$的一系列transfer functions。

首先是方向$D$。很明显，常量传播分析应该是一个前向分析，因为对于每个节点来说，需要考虑的是前驱节点对它的影响。

接下来讨论格$L$，它的值域$V$如下所示，由UNDEF、常量和NAC（not a constant）组成：

graph TD A("UNDEF") --> B("-2") A --> C("-1") A --> D("0") A --> E("1") A --> F("2") B --> G("NAC") C --> G D --> G E --> G F --> G style A fill:#b12318 style G fill:#1d8daa

操作符是meet $\lceil \rceil$，它需要根据不同情况执行不同的操作：

  • $\text{NAC} \lceil \rceil v = \text{NAC}$
  • $\text{UNDEF} \lceil \rceil v = v$
  • $c \lceil \rceil v =\ ?$
    • $c \lceil \rceil c = c$
    • $c_{1} \lceil \rceil c_{2} = \text{NAC}$

上述操作完全是根据实际需求来定义的。例如，我们并不关心未初始化的变量（UNDEF）。

接下来考虑转换函数。给定一个语句$s: x = …$，我们将其转换函数定义为：

$$ F: OUT[s] = gen\ \cup\ (IN[s] - \lbrace (x, \underline{\ \ } ) \rbrace) $$

下面来看如何针对三类不同的语句生成$gen$：

  • $s: x = c$，则$gen = \lbrace (x,c) \rbrace$
  • $s: x = y$，则$gen = \lbrace (x,val(y)) \rbrace$
  • $s: x = y\ op\ z$，则$gen = \lbrace (x,f(y,z)) \rbrace$

其中$f(y,z)$定义如下：

$$ f(y, z) = \begin{cases} val(y)\ op\ val(z) &\text{if val(y) and val(z) are constants} \\ \text{NAC} &\text{if val(y) or val(z) is NAC} \\ \text{UNDEF} &\text{otherwise} \end{cases} $$

另外，如果$s$不是一个赋值语句，那么转换函数$F$不起作用，相当于空函数即可。

下面这个小例子说明，常量传播分析是not distributive的：

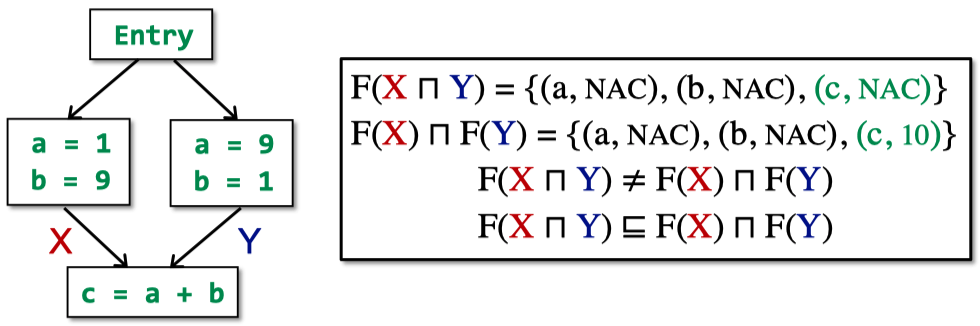
image-20230316181946793

Worklist算法

OK，最后来看一下worklist算法。

思想其实很简单，就是维护了一个worklist，根据worklist是否为空判断迭代是否停止，只把OUT变化的节点的后继加入到worklist中，从而不必每次迭代都遍历CFG所有节点。

Worklist算法的伪代码如下图所示：

image-20230316192616877

总结与思考

至此，数据流分析的理论部分结束。本节课，我们学习了如何将迭代算法与不动点定理关联、如何在格的视角下理解may/must分析、MOP和分配性、常量传播分析和Worklist算法。最后两部分其实也可以算作数据流分析应用了。

这两节理论课不分伯仲。个人感觉上节课的内容更复杂，但是这节课的内容更抽象。

话不多说，A2实验见。