前言

上节课，我们初步学习了C.S.的指针分析的一些概念，如call-site sensitivity、cloning-based context sensitivity和context-sensitive heap等。在此基础上，我们进而学习了C.S.的指针分析规则——总体而言，它与C.I.的指针分析规则十分相似，只是多了上下文而已。然而，也正是因为多了上下文，我们引入了一个新的$Select$函数来为目标方法选择对应的上下文。$Select$函数对于C.S.分析来说非常重要。

本节，我们将继续学习C.S.的指针分析。首先，我们将学习C.S.指针分析算法；第二部分，我们将会看到不同类型的C.S.处理方法。

C.S.指针分析算法

回顾之前学过的C.I.的指针分析，可以发现，PFG的建立过程与指针指向信息在PFG上的传播过程是相互依赖的。这一点在C.S.指针分析中也适用。

在第九节中相关定义的基础上，我们将C.S. PFG上的一个节点定义为：

$$ \text{CSPointer} = (C \times V) \cup (C \times O \times F) $$

也就是说，C.S. PFG上的一个节点代表一个C.S.变量或一个C.S.抽象对象的域。类似地，C.S. PFG的边自然是$\text{CSPointer} \times \text{CSPointer}$了。例如，边$c:a \rightarrow c’:b$表示$pt(c:a)$中的对象可传播到$pt(c’:b)$中。

我们在上节课给出的规则表上新增一个C.S. PFG边的示意：

种类 语句 规则 PFG边
New i: x = new T() $\frac{}{c:o_{i} \in pt(c:x)}$ N/A
Assign x = y $\frac{c’:o_{i} \in pt(c:y)}{c’:o_{i} \in pt(c:x)}$ $c:x \leftarrow c:y$
Store x.f = y $\frac{c’:o_{i} \in pt(c:x),\ c’’:o_{j} \in pt(c:y)}{c’’:o_{j} \in pt(c’:o_{i}.f)}$ $c’:o_{i}.f \leftarrow c:y$
Load y = x.f $\frac{c’:o_{i} \in pt(c:x),\ c’’:o_{j} \in pt(c’:o_{i}.f)}{c’’:o_{j} \in pt(c:y)}$ $c:y \leftarrow c’:o_{i}.f$
Call l: r = x.k(a1, ..., an) 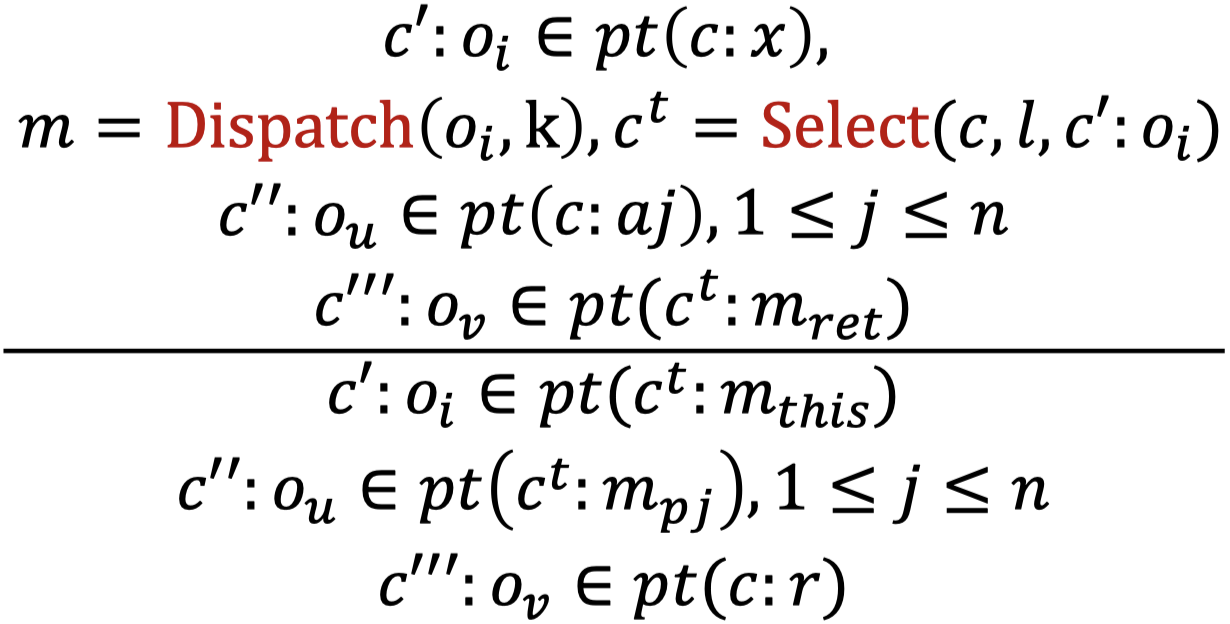image-20230406215641893 $c:a1 \rightarrow c^{t}:m_{p1} \\ … \\ c:an \rightarrow c^{t}:m_{pn} \\ c:r \leftarrow c^{t}:m_{ret}$

OK，前菜结束，上算法：

image-20230409161534157

与C.I.的算法对比来看，C.S.的算法只是多了上下文限定（类似$c:$这样的部分）和$Select$函数。两个底层函数$AddEdge$和$Propagate$则在两个算法中完全相同——事实上，它俩从过程内C.I.指针分析开始就没变过。

不同类型的C.S.处理方式

我们注意到，前面一小节结束后，竟然没有例子，这似乎不太符合老师们的授课风格。其实，例子就在本小节后面。毕竟，我们一直没有学习$Select$的实现方式，而事实上这里边有很多道道。换句话说，“上下文如何选择”是一个值得深入思考的问题。选择不同，得到的算法和结果也可能不同。

常见的C.S.处理方法有三种：call-site sensitivity、object sensitivity和type sensitivity。

在学习这些处理方法之前，再看一下$Select$函数： $$ c^{t} = Select(c, l, c’:o_{i}) $$

其中，$c$是caller context，$l$是call site，$c’:o_{i}$是带有堆上下文的消息接收对象（一种看待OOP的视角：调用某个对象的方法，其实就是给该对象发消息）。

$Select$函数的三个参数并非每次都是必需的。具体需要传入什么参数，要看C.S.处理方法是什么。我们还可以把C.I.指针分析纳入到C.S.中来，前者只是后者的一种特殊情况，相应的$Select$每次返回空（无上下文）即可。

OK，下面我们就来研究一下不同的C.S.处理方法。

Call-Site Sensitivity

Call-site sensitivity由Olin Shivers于1991年在他的博士论文Control-Flow Analysis of Higher-Order Languages中提出。其思想是，每个上下文都是一个call sites列表（调用链），在方法调用时，将call site加入到caller context中，作为callee context，实质上就是调用栈的抽象： $$ Select(c, l, \underline{\ \ }) = \lbrack l’,\ …\ , l’’, l \rbrack\ where\ c = \lbrack l’,\ …\ , l’’ \rbrack $$ 因为上下文形如一个字符串，因此call-site sensitivity也叫做call-string sensitivity，或者$k$-CFA。

$k$-CFA全称是k-Limiting Context Abstraction。顾名思义，就是要限制上下文的长度。Call-site sensitivity的特性导致这样产生的上下文可能会非常长，比如递归的情况。一方面，我们要确保指针分析能够终止；另一方面，我们不希望上下文过长，也没必要过长。

因此，我们为上下文长度设置一个上界$k$——每个上下文只包括前$k$个call sites，更早的就丢掉。实践中，$k$通常小于3。另外，方法上下文和堆上下文可能采用不同的$k$。

下面，我们来看一个1-CFA的例子（未考虑C.S. heap，并忽略了C.id(Number)的this变量）：

01 class c {
02     static void main() {
03         C c = new C();
04         c.m();
05     }
06
07     Number id(Number n) {
08         return n;
09     }
10     void m() {
11         Number n1, n2, x, y;
12         n1 = new One();
13         n2 = new Two();
14         x = this.id(n1);
15         y = this.id(n2);
16         x.get();
17     }
18 }

初始化：

WL: []
PFG:
CG: {}
RM: { []:C.main() }

最终处理结果如下：

PFG:
[]:c{o_3}  [4]:C.m_this{o_3}
[4]:n1{o_12} -> [14]:n{o_12} -> [4]:x{o_12}
[4]:n2{o_12} -> [15]:n{o_13} -> [4]:y{o_13}

CG: {
  []:4 -> [4]:C.m(),  [4]:14 -> [14]:C.id(Number),
  [4]:15 -> [15]:C.id(Number), [4]:16 -> [16]:One.get()
}

中间的过程可以自己一步步推导得到，或者参考谭添老师的课件。另外，如果对比C.S.和C.I.的结果，我们将发现，C.S.的结果更为精确。

Object Sensitivity

OK，接下来是第二种C.S.处理方式：对象敏感性。这种处理方式在2002年的一篇论文Parameterized Object Sensitivity for Points-to Analysis for Java被提出，思路与前一种截然不同——用抽象对象（由对象allocation sites表示）列表来构成上下文，而非call sites构成。在方法调用时，将接收者对象和它的heap context作为callee context。相应的$Select$函数如下：

$$ Select(\underline{\ \ }, \underline{\ \ }, c’:o_{i}) = \lbrack o_{j},\ …\ , o_{k}, o_{i} \rbrack\ where\ c’ = \lbrack o_{j},\ …\ , o_{k} \rbrack $$

由于抽象对象由allocation sites表示，因此这种处理方式也叫做allocation-site sensitivity。

我们直接来看一个1-CFA和1-object对比的例子吧：

image-20230409224741874

在这个例子中，似乎object sensitivity更为准确。Object sensitivity其实模拟的就是Java语言运行时的动态处理过程。具体到这个例子而言，不同的上下文都可能流经call-site [12]，然而1-CFA导致历史上下文被丢掉了，准确度自然下降。增加$k$-CFA的$k$可以缓解问题，但是并不能完全解决——只要类似的调用层数比$k$大，这样的问题都会出现。

然而，object sensitivity一定比call-site sensitivity更准确吗？不见得。用object sensitivity来处理一下上一小节中的那个例子，将结果与call-site sensitivity的结果做对比，可以发现，这次反而object sensitivity是不准确的那个：

image-20230409225937419

理论上，call-site sensitivity和object sensitivity的准确性是不可比较的。

实践中，在处理OOP时，object sensitivity一般比call-site sensitivity的效果更好（具体到个例则另说）。李樾、谭添老师在2020年发表的论文A Principled Approach to Selective Context Sensitivity for Pointer Analysis也证实了这一点（下图中，数值越小表示越好）：

image-20230409230743310

Type Sensitivity

第三种C.S.处理方式是类型敏感性。从名字上我们就大概能猜出来它的思路，甚至能够猜到它的准确性可能会比object sensitivity低一些，但是效率会高一些。所谓类型敏感性，就是使用包含allocation site的“类型”和堆上下文作为callee object。其$Select$函数如下：

$$ Select(\underline{\ \ }, \underline{\ \ }, c’:o_{i}) = \lbrack t’,\ …\ , t’’, InType(o_{i}) \rbrack\ where\ c’ = \lbrack t’,\ …\ , t’’ \rbrack $$

这种处理方式在2011年的一篇论文Pick YourContexts Well: Understanding Object-Sensitivity被提出。

需要注意的是，是包含allocation site的类型，不是接收对象的类型。例如，在下面这段代码中，$InType(o_{3}) = X$，不是$Y$：

1 class X {
2     void m() {
3         Y y = new Y();
4     }
5 }

严谨地说，在相同k-limiting条件下，type sensitivity的准确性不高于object sensitivity。下面是将call-site、object和type三种sensitivity处理方式放在一起进行比较的结果，同样来自前面提到的李樾、谭添老师的论文：

image-20230409232120932

总体而言，对于OOP指针分析，就准确性来说，object > type > call-site；就效率来说，type > object > call-site。

总结与思考

这一节我们学了很多东西，非常非常有意思，尤其是不同的上下文敏感处理方式。个人觉得，这些处理方式是因地制宜、与语言本身息息相关的。如果以后我们要处理C语言及其他非OOP（或至少非严格OOP）的语言，也许情况又要变化了。

总之，非常有意思。