前言
这是南大软件分析课程最后两节视频课的笔记。这两节课又换成了李樾老师讲。
倒数第二节课,我们将学习上下文无关语言(context-free language,简称CFL)可达性的概念和一种新的程序分析框架——IFDS,它用于解决满足Interprocedural、Finite、Distributive、Subset特性的分析问题;最后一节课,我们将了解程序分析目前在Soundness上遇到的问题,以及Soundiness的概念。
Feasible and Realizable Paths
现实中,一个方法的CFG可能会非常复杂。因此,我们希望排除CFG中实际执行时不会经过的路径(infeasible paths),从而降低复杂性。然而,从普遍意义上来说,给定一个路径,我们是无法判断它是否为infeasible的。
例如,在下图中,如果结合常识,我们将发现foo函数中的age < 0这个分支可能是不会经过的,但是程序分析却无法判定这一点。
然而,这并不意味着我们对所有infeasible paths都束手无策。像下面的CFG中从Call foo(30)到Exit foo再到x = Return foo这种call与return不匹配的情况,我们还是有办法处理的。
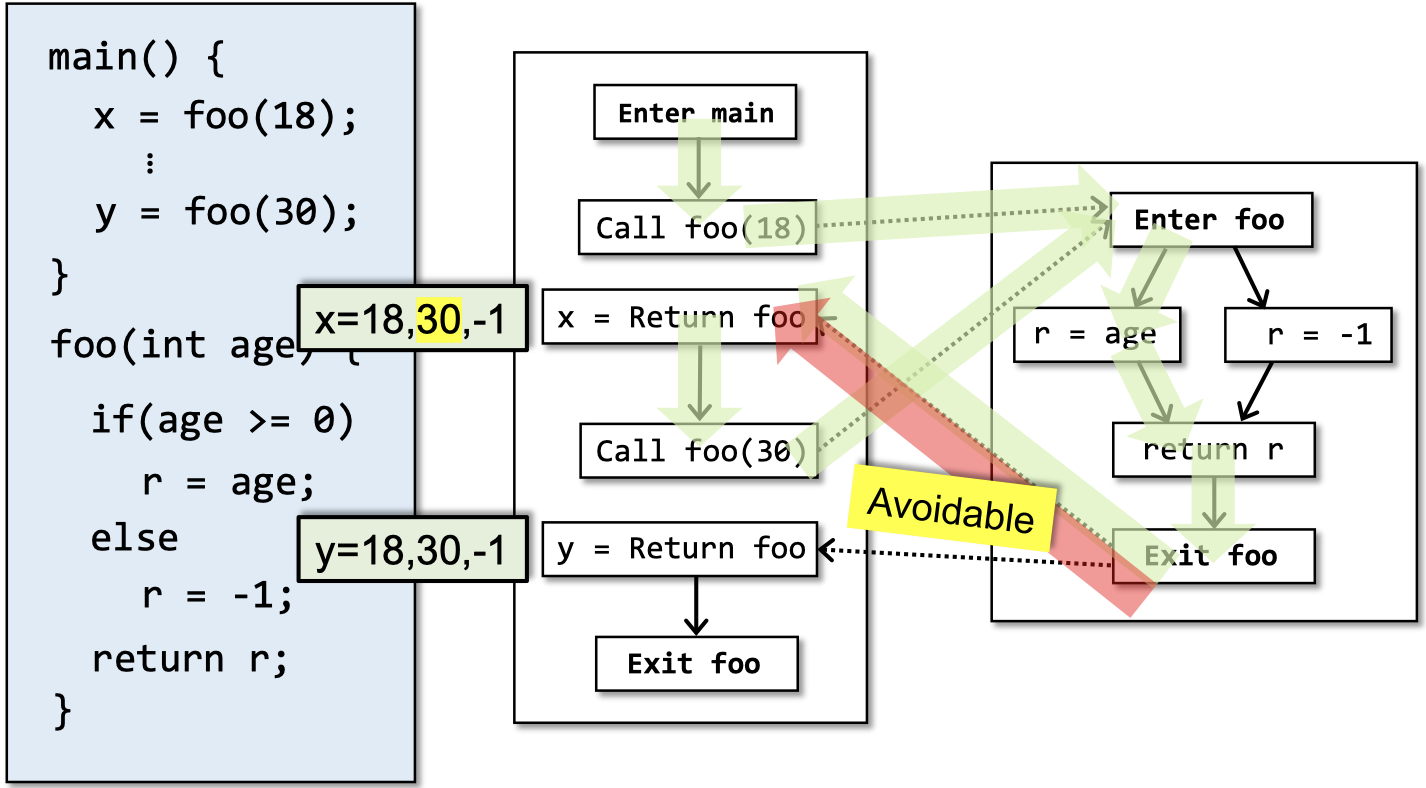
我们首先定义realizable paths这个概念:它指的是程序中return和call相匹配的路径。注意,realizable paths可能是不可执行的,但是unrealizable paths一定是不可执行的。我们的目标是,识别出程序中的realizable paths,从而排除unrealizable paths。
那么,如何识别realizable paths呢?我们需要引入CFL-Reachability。
CFL-Reachability
CFL即context-free language,上下文无关语言。一个路径连接了CFG上的节点A和B,或者说B是从A可达的,当且仅当从A到B的路径的边的标签连接起来构成的字符串符合上下文无关语言文法规则。
注意,一个用语言L写的合法句子必须遵从语言L的文法。上下文无关语言就是由上下文无关文法(context-free grammar,简称CFG,为避免与control flow graph的缩写混淆,我们还是称其为上下文无关文法)生成的。
上下文无关文法是一种形式文法,它的产出具有如下形式:
$$ S \rightarrow \alpha $$
其中,$S$是一个非终止符,$\alpha$可以是一个由终止符和(或)非终止符构成的字符串,或者为空。对应的生成规则有如下两条:
$$ S \rightarrow aSb \\ S \rightarrow \varepsilon $$
所谓“上下文无关”,意味着$S$可以被$aSb$或$\varepsilon$替换,无论$S$出现在哪里。
接着来看CFL-Reachability,它是一个基于CFL描述的不完全括号匹配问题,具体来说:
- 在每个右括号$)_{i}$之前,都必须有一个对应的左括号$(_{i}$匹配。但是反过来则不必满足——每个左括号$(_{i}$后面不一定要跟着一个右括号$)_{i}$。
- 对于每个call site $i$来说,我们将其call edge和return edge分别标记为$(_{i}$和$)_{i}$。
- 将CFG中剩下的边标记为符号$e$。
在此基础上,我们说,一个路径是realizable的,当且仅当该路径构成的句子能够用语言$L(realizable)$描述,该语言的文法规则如下图中间部分所示:
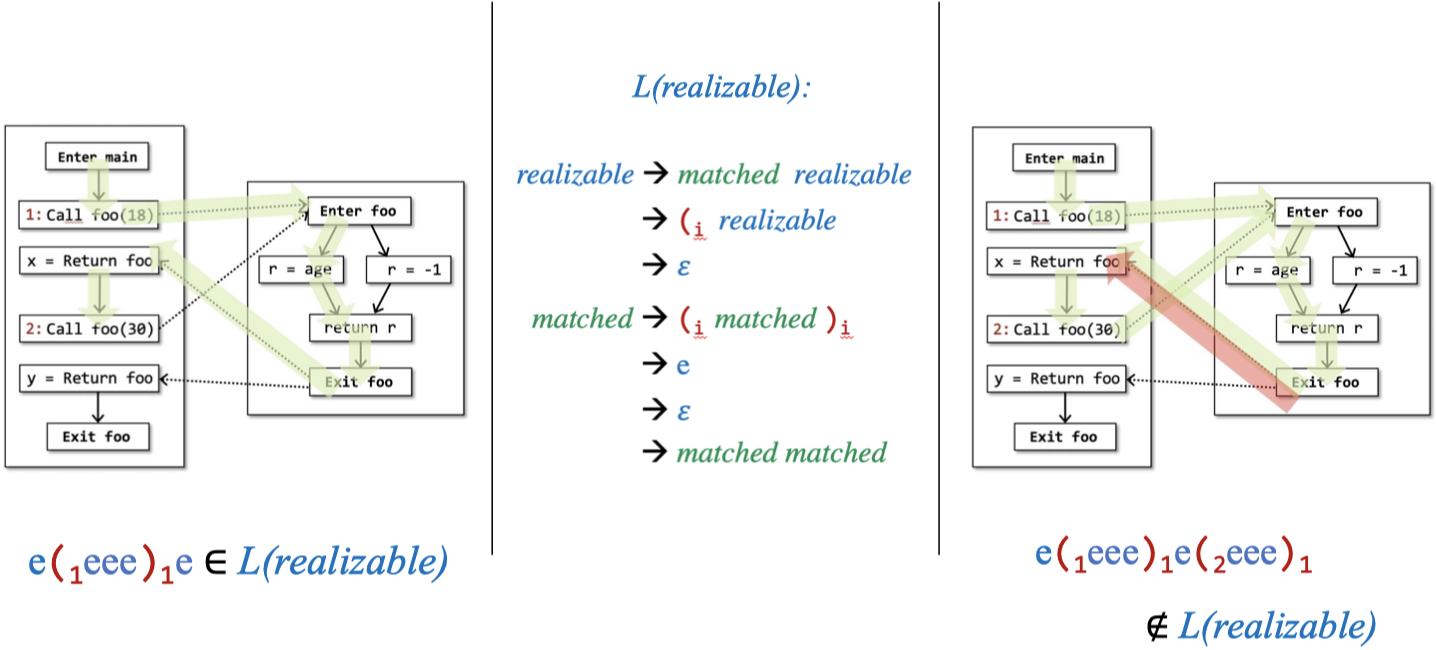
上图中左右两侧分别是能够用$L(realizable)$描述和不能用$L(realizable)$描述的两个例子。
IFDS简介
了解了CFL- Reachability,我们来学习IFDS,它是一个基于图可达性的程序分析框架,出自1995年的论文Precise Interprocedural Dataflow Analysis via Graph Reachability。IFDS用于处理在有限(finite)域上的过程间(interprocedural)数据流分析,且相应的flow functions必须具有可分配特性(distributive),它给出的解是meet-over-all-realizable-paths(MRP)的。
MRP是什么呢?我们在《南大软分课程笔记|06 数据流分析理论》中学习过MOP,这里简单回顾一下(之前应用在节点上,现在我们应用在边上,思想是一样的):
我们将路径$p$的path function记作$pf_{p}$,它是由$p$上所有边的flow functions构成的复合函数:
$$ pf_{p} = f_{n} \circ\ …\ \circ f_{2} \circ f_{1} $$
相应地,对于每个节点$n$来说,$MOP_{n}$提供了$Paths(start, n)$的meet-over-all-paths的解,其中$Paths(start, n)$表示从开始节点到节点$n$的路径集合:
$$ \text{MOP}_{n} = \bigsqcup_{p\ \in\ \text{Paths}(start, n)} pf_{p}(\bot) $$
类似地,$MRP_{n}$则表示meet-over-all-realizable-paths,其中$RPaths(start, n)$表示从开始节点到节点$n$的realizable路径集合:
$$ \text{MRP}_{n} = \bigsqcup_{p\ \in\ \text{RPaths}(start, n)} pf_{p}(\bot) $$
很明显,$MRP_{n} \preccurlyeq MOP_{n}$。
在此基础上,我们来理解LFDS。可能有点抽象难懂,没关系,一点一点来。接下来进入“抽象难懂环节” :-)
给定一个程序$P$和一个数据流分析问题$Q$:
- 为$P$构建一个supergraph $G^{\star}$,并基于$Q$为$G^{*}$中的每个边定义flow function。
- 为$P$构建一个exploded supergraph $G^{\sharp}$,构建方式是将flow functions转化为表示关系(representation relations)图。
- 问题$Q$可以通过在$G^{\sharp}$上应用Tabulation算法,作为图可达性问题被解决。其实质就是找出所有的MRP解。
我们说,如果定义$n$是一个program point,data fact $d \in MRP_{n}$,当且仅当在$G^{\sharp}$中从$\langle s_{main}, 0 \rangle$到$\langle n, d \rangle$有一条realizable path。
下图展示了上述三个步骤。该图仅供复习用,在没有完整学过这部分的情况下,可能看不懂下面这个图片,这是正常的。
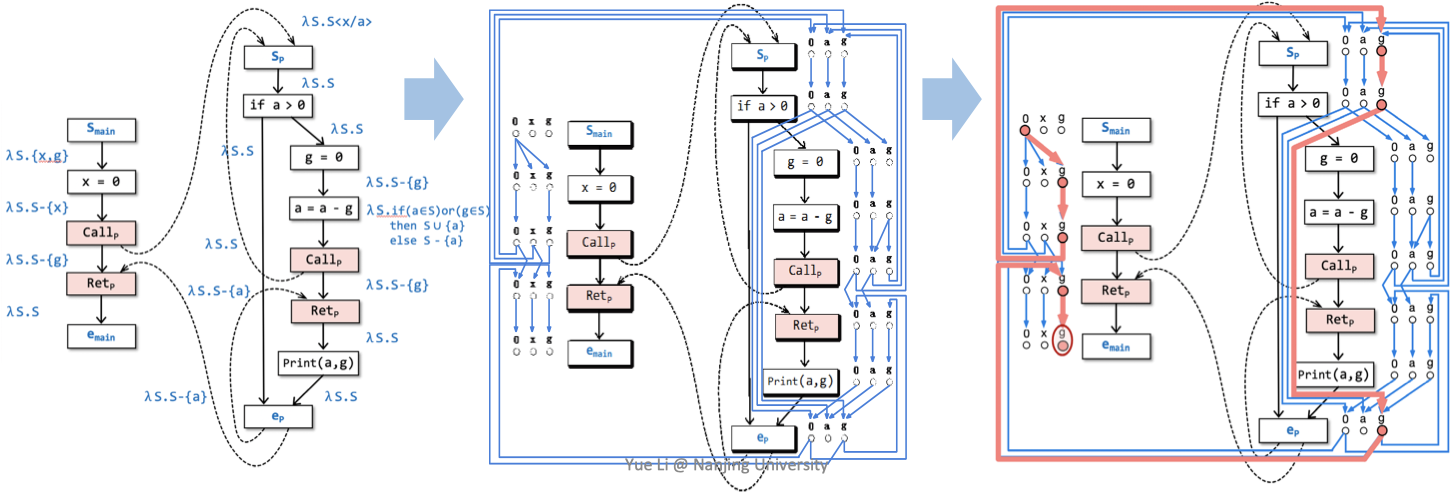
接下来我们来逐一学习。
Supergraph和Flow Functions
首先是supergraph。在IFDS中,一个程序由一个supergraph表示,记作$G^{\star} = (N^{\star}, E^{\star})$。其实,$G^{\star}$很好理解,它由程序中所有过程的程序流图组成($G_{1}$,$G_{2}$等),每个程序流图包含一个开始节点$s_{p}$和一个退出节点$e_{p}$。一次过程调用由一个调用节点$Call_{p}$和一个return-site节点$Ret_{p}$表示。
$G^{\star}$中的每个过程调用包含三条边:
- 一个从$Call_{p}$到$Ret_{p}$的过程间call-to-return边
- 一个从$Call_{p}$到被调用过程的$s_{p}$的过程间call-to-start边
- 一个从被调用过程的$e_{p}$到$Ret_{p}$的exit-to-return-site边
下面是一个supergraph的示例:
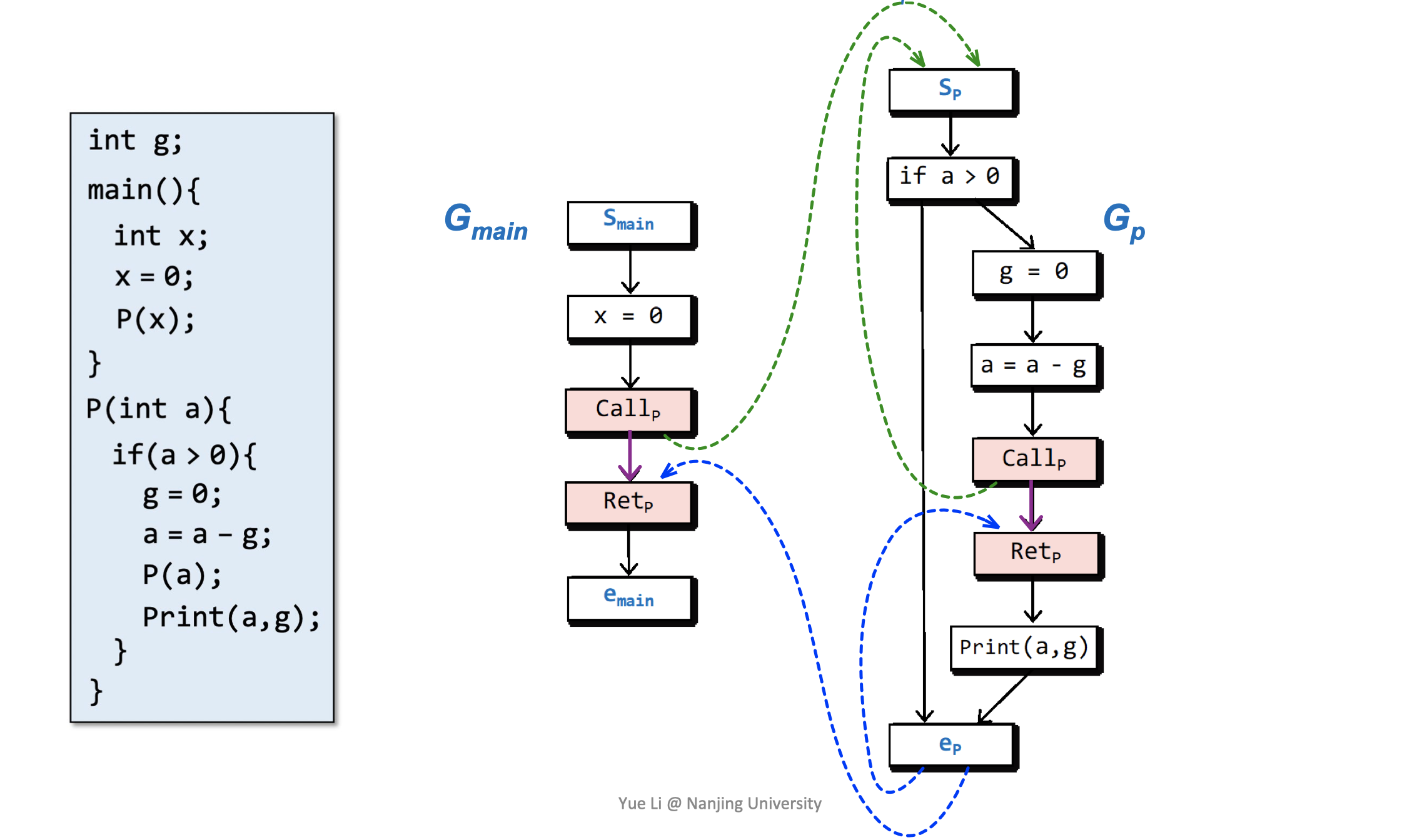
接着,我们来看flow functions。从之前学习过的数据流分析应用中可以知道,不同应用的transfer function可能是不一样的。Flow functions也是如此。这里,我们以“可能的未初始化变量”这一分析来介绍如何设计IFDS中的flow functions。
“可能的未初始化变量”分析指的是,对于每个节点$n \in N^{\star}$,确定在执行流到达$n$之前未初始化的变量集合。
我们采用lambda函数的形式定义flow functions:$\lambda\ e_{param} . e_{body}$。例如,$\lambda\ x . x+1$就是一个lambda函数,$(\lambda\ x . x+1)3$表示为该函数传入参数为3,它将返回4。
在supergraph的基础上,我们为“可能的未初始化变量”分析定义flow functions:
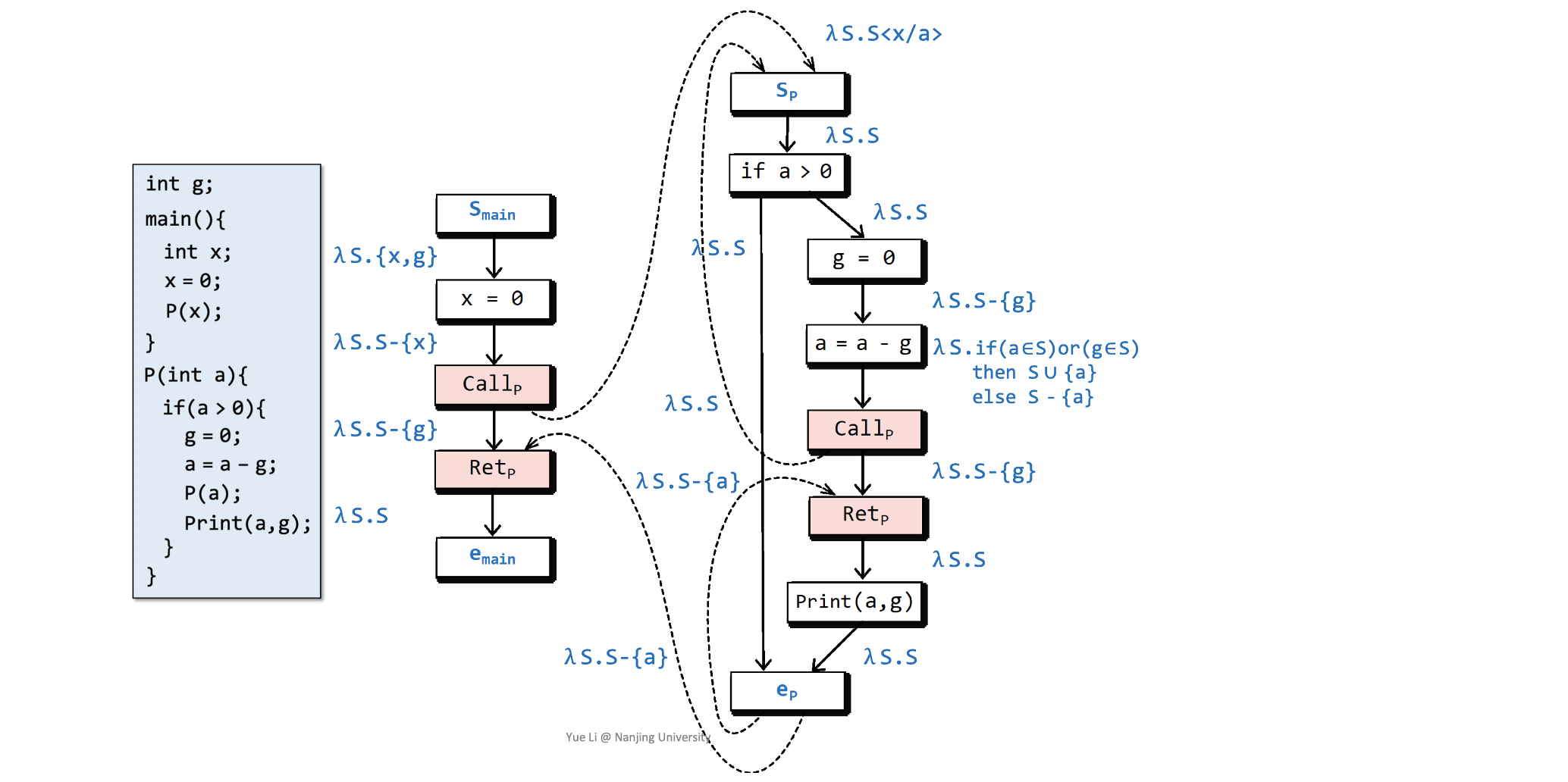
Exploded Supergraph和Tabulation算法
OK,现在有了supergraph和flow functions,我们接下来构建exploded supergraph $G^{\sharp}$,构建方式是将flow functions转化为representation relations。每个flow function可以用一个图来表示,图中有$2(D+1)$个节点,最多有$(D+1)^{2}$条边,$D$是data facts的有限集。
我们定义$R_{f} \subseteq (D \cup 0) \times (D \cup 0) $是flow function $f$的二元representation relation,具体规则如下:
$$ R_{f} = \lbrace (0, 0) \rbrace \ \cup \ \lbrace (0, y) \ | \ y \in f(\empty) \rbrace \ \cup \ \lbrace (x, y) \ | \ y \notin f(\empty) \ \text{and} \ y \in f(\lbrace x \rbrace) \rbrace $$
其中,这三个用$\cup$连接的部分分别对应$0 \rightarrow 0$、$0 \rightarrow d_{1}$和$d_{1} \rightarrow d_{2}$三条边。
下面是4个flow functions到representation relations的转化示例:
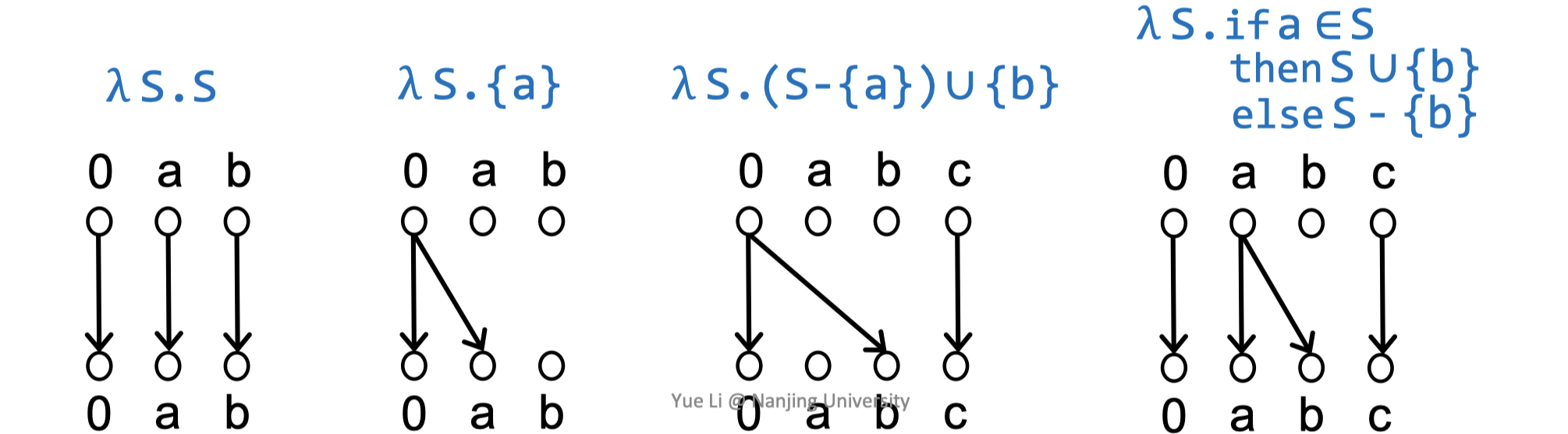
Exploded有“爆裂的”之意。Exploded supergraph $G^{\sharp}$指的是,$G^{\star}$中的每个节点$n$都“爆裂”为$G^{\sharp}$中的$D+1$个节点,$G^{\star}$中的每个$n_{1} \rightarrow n_{2}$的边也“爆裂”为$G^{\sharp}$中的representation relation(借助flow funciton转化)。
在传统的数据流分析中,我们通常通过检查data fact $a$是否在$OUT[n_{i}]$中来判断$a$在program point $p$处是否有效。Data facts通过复合的flow functions传播。可达性也因此取决于$OUT[n_{i}]$的最终内容。
在IFDS中,我们则通过检查是否有一条从$\langle s_{main}, 0 \rangle$到$\langle n_{i}, a \rangle$的realizable path来判断可达性。
其中,值得注意的是每个representation relation中默认添加的$0 \rightarrow 0$这条边。只有添加了这条边,不同representation relation之间才能连接起来,得到正确的结果。
下图中左侧是我们前面得出的$G^{\star}$,右侧则是据此构建出来的$G^{\sharp}$:
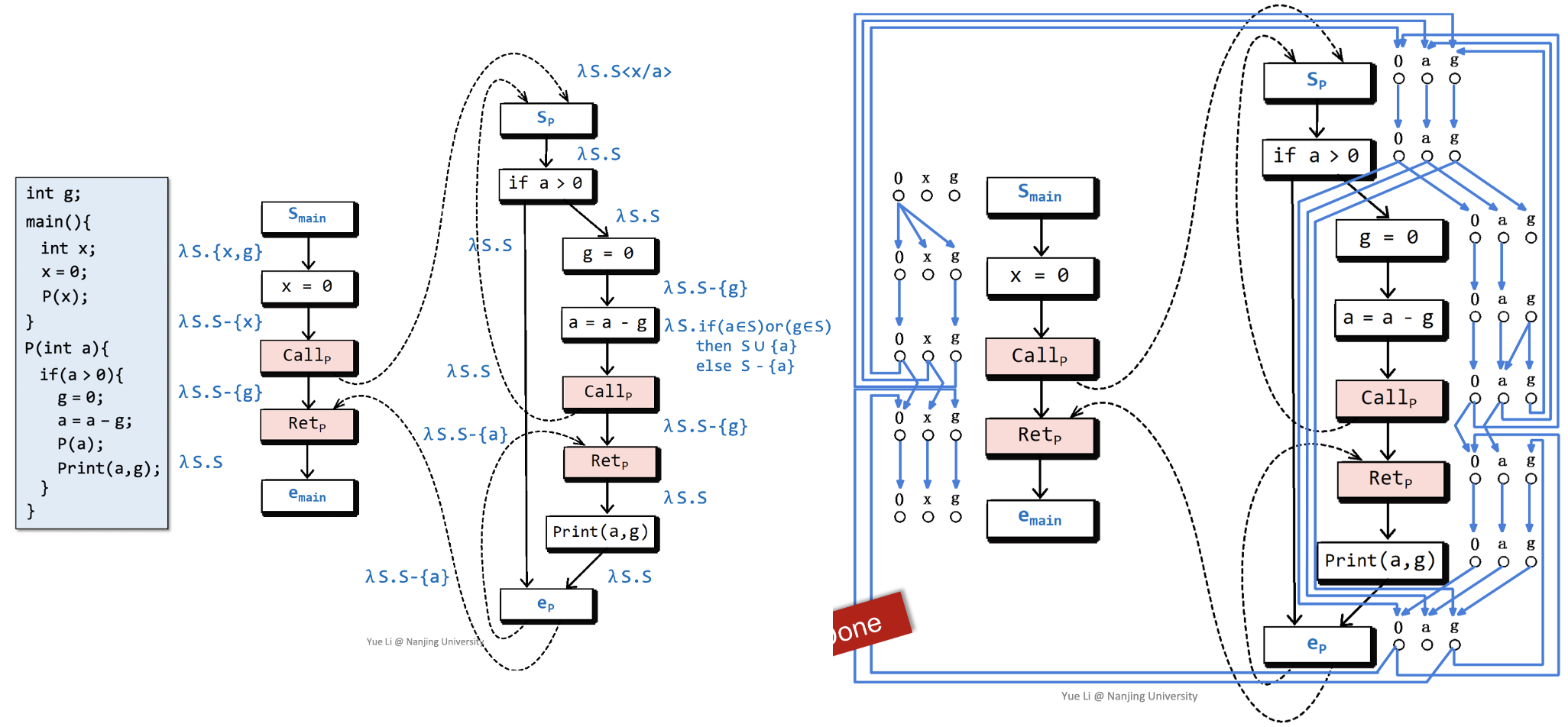
我们可以基于$G^{\sharp}$来手动得出一些可达性的结论。下图中,左侧部分是可达的一种情况,右侧是不可达的一种情况:
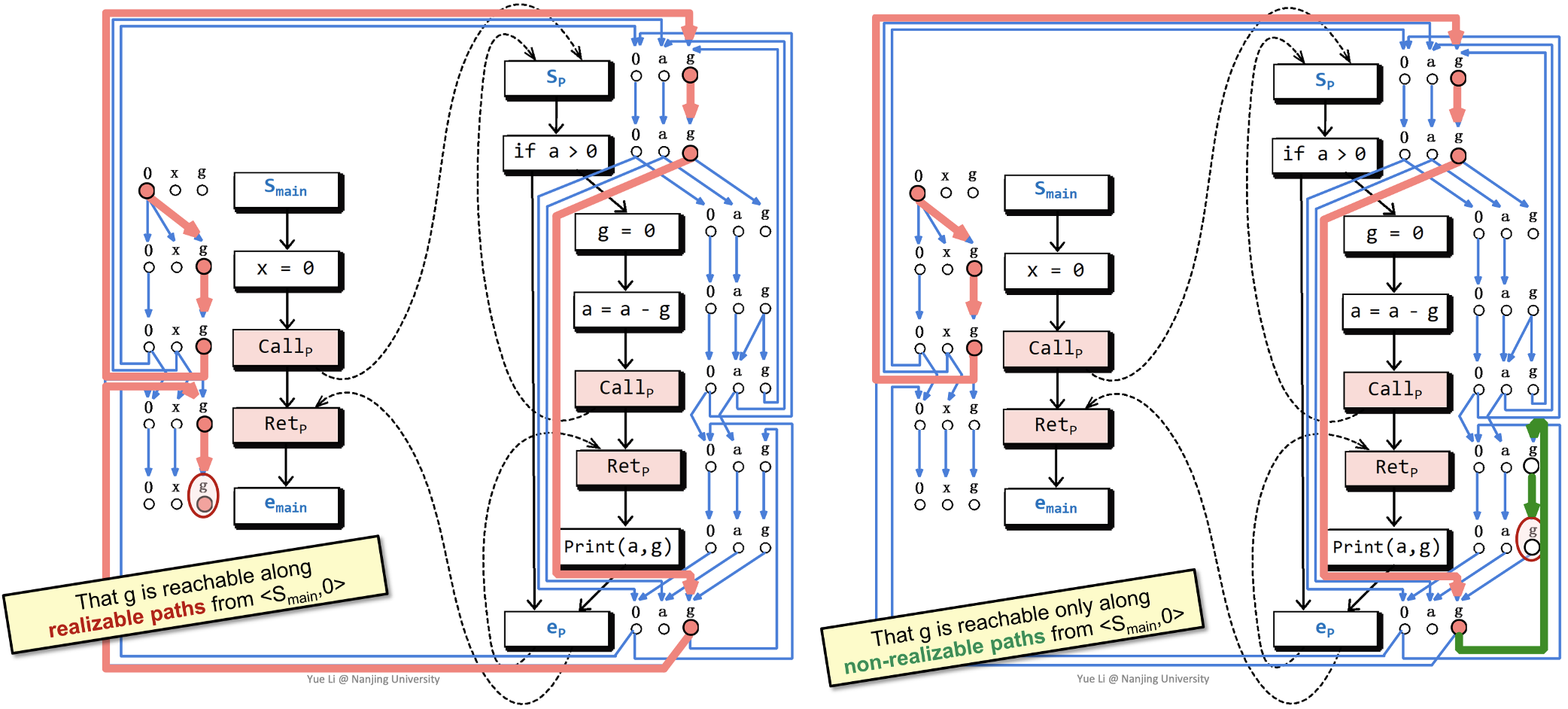
最终,完整地给出MRP的解还需要Tabulation算法,该算法将把所有从$\langle s_{main}, 0 \rangle$到$\langle n, d \rangle$有一条realizable path的$\langle n, d \rangle$标注出来(如下图中蓝色点所示):
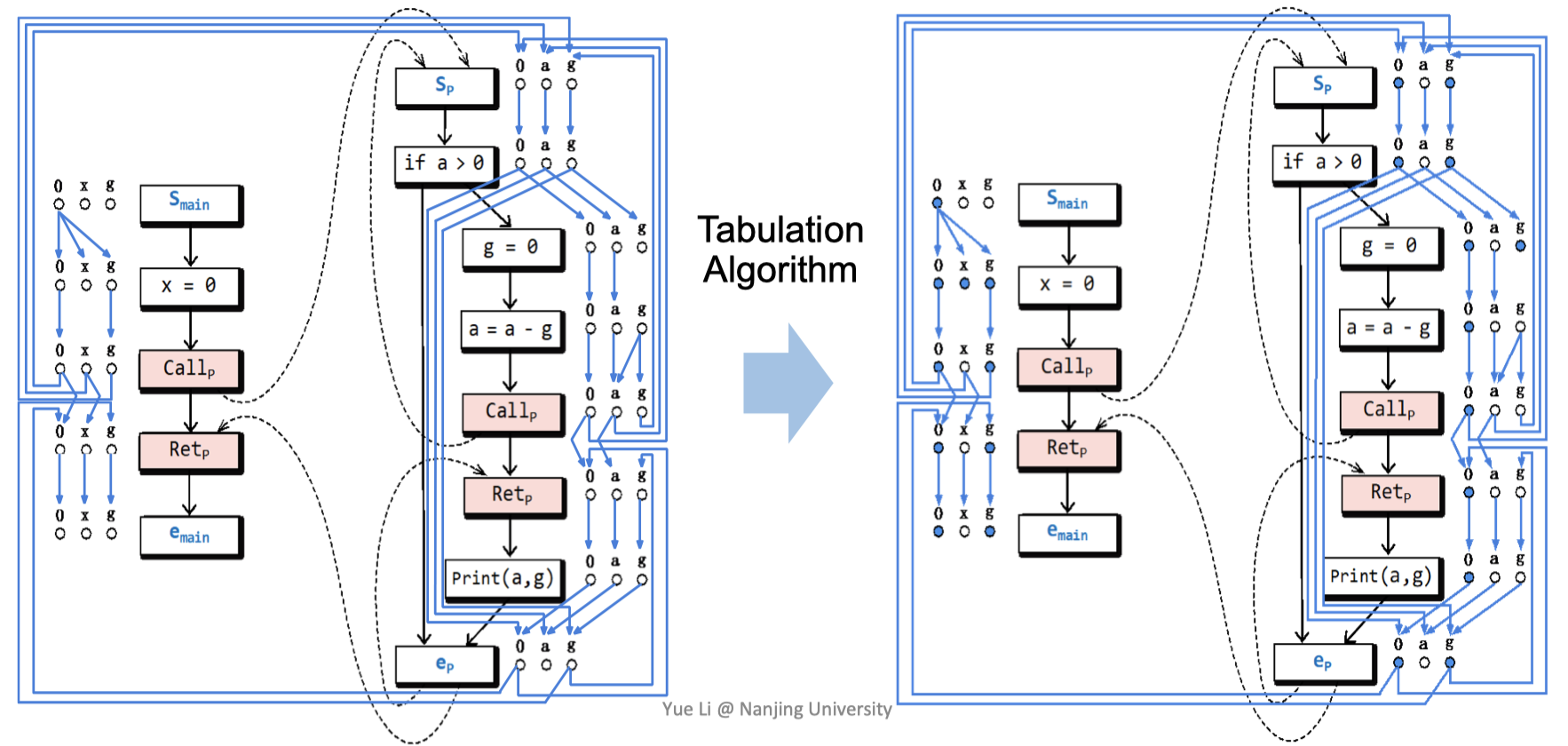
下面是GPT-4对Tabulation算法的介绍:
Tabulation算法是一种动态规划技术,用于通过将问题分解成较小的、重叠的子问题,并将结果存储在表格中以实现高效重用,从而解决问题。这种方法对于优化和组合问题特别有效,因为它有助于避免冗余计算并加速解决过程。
Tabulation算法的基本思想是构建一个表示问题解空间的表格(通常是一个二维数组)。然后,算法通过迭代地填充表格,使每个条目对应于特定子问题的解决方案。通常通过分析表格中的值来找到整个问题的最终解决方案。
Tabulation算法与另一种动态规划技术(称为Memoization)的区别在于,Tabulation算法采用自底向上的方法,先解决较小的子问题,然后构建整个问题,而Memoization采用自顶向下的方法,通过将整个问题分解成较小的子问题并缓存其结果来解决问题。
一个可以使用Tabulation算法解决的问题示例是经典的0/1背包问题。该问题旨在确定在限定重量的背包中可以装入的物品的最大价值,给定每个物品的重量和价值。通过构建一个表格并迭代填充它,算法可以有效地计算出问题的最优解。
这里附上一张bsauce对该算法的注释图:

IFDS的可分配性(Distributivity)
IFDS中的I、F、S都比较好理解,那么D对应的“可分配”又如何理解呢?
结合例子来看。事实上,之前我们做过的常量传播(常量传播的domain是无限的。即使有限,也不行)和指针分析都不能直接用IFDS来处理。为什么呢?
首先回顾一下,所谓distributivity,就是
$$ F(x \wedge y) = F(x) \wedge F(y) $$
IFDS中的每个flow function每次处理的输入data fact都只有一个,而常量传播中的一次处理可能会依赖多于一个data fact的情况,例如$z = x + y$,我们需要同时给出$x$和$y$的情况作为输入。在IFDS中,我们没法定义一个同时依赖$x$和$y$的$F$。因此,类似的分析都不能用IFDS来做。
对于指针分析来说,由于IFDS缺少别名(alias)信息,最终也可能会造成结果不准确:
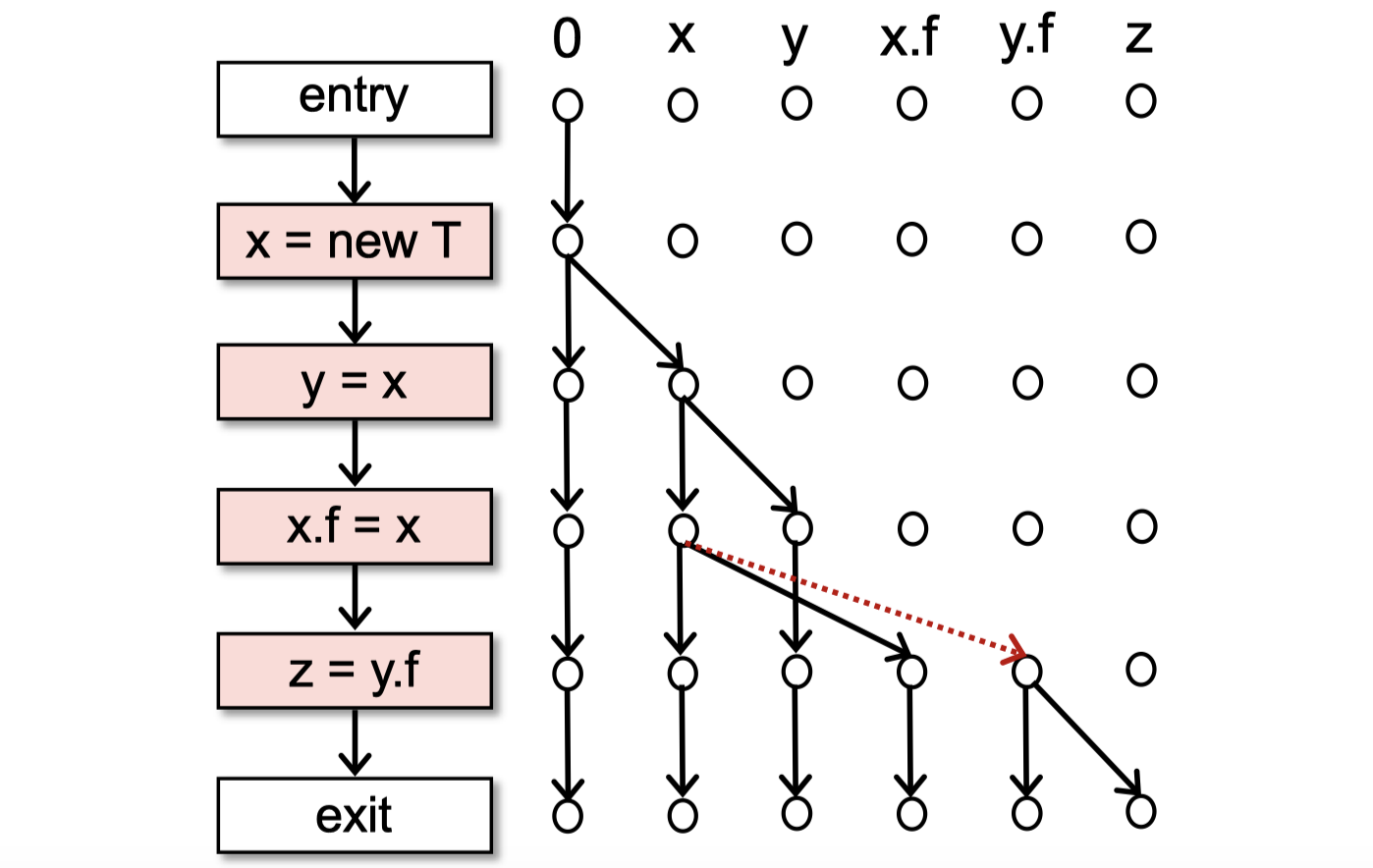
然而,我们如果想要在IFDS中获取别名信息,就要同时考虑多个data facts,如$x$和$y$,这与前面常量传播的不适用情况一致。
Soundiness
现在,我们来记录一下最后一节课学习的知识。
第一节课中,我们曾学习过sound和complete的概念。通常情况下,我们总是选择牺牲completeness,保全soundness。Soundness是一个理想的状态——捕获程序的全部行为、分析出所有可能的执行结果。事实上,无论是在学术界还是工业界,全程序分析通常都是unsound,这是因为现代编程语言通常都有一些难以进行静态分析的hard features。例如,Java中有反射(reflection)、native code、动态类加载等;JavaScript中有eval函数,文档对象模型(DOM)等;C/C++中有指针运算、函数指针等。
因此,通常情况下,学术界和工业界有一些现象和做法:
- 一个所谓的sound的静态分析,只是在实现上有一个sound core,也就是对绝大多数语言特性做了over-approximated处理,但是某些难以分析的部分则是under-approximated处理。
- 略去hard language features的处理,或者只是在实现或评估部分简单地提一下。
- 未能考虑到hard language features,导致分析结果有问题。
鉴于这些现象,2015年,领域内人士提出了Soundiness一词,类比Truthiness(指某个truth只是某些人相信的,但没有事实或证据支持),对应的形容词是soundy,希望大家能够用合适的词汇准确描述自己的研究。现在我们可以说,一个sound的分析需要捕获全部动态行为,这通常是不可能实现的;一个soundy的分析希望去捕获全部动态行为,但是对于部分hard language features的unsoundly处理给出了解释;一个unsound的分析是主观上忽略了部分行为,从而达到更好的效率、准确性或可行性。
接着,作为示例,李樾老师分析了Java的反射和native code两个hard language features,探讨为什么它们难于分析,以及学术界的研究进展。事实上,反射部分最先进的研究是李樾和谭添老师做的。这可以说是顶级“凡尔赛”了,但是哪个学生不希望听到老师说课程最前沿的部分是自己做的呢?换句话说,能听顶尖工作的作者讲的该领域的课应该是一种荣幸。
简单来说,Java反射机制难于进行静态分析的原因是,Class.forName(cName)、c.getMethod(mName, ...)等方法的参数可能是运行时才能确定的(来自网络、配置文件、用户输入等),静态分析很难获得这些参数信息,进而难于确定对应的类和方法。学术界目前的解决方法可以归为三类:
- 字符串常量分析+指针分析(论文链接)。这个思路比较直观,但是也存在明显的问题——如果字符串的值确实是运行时才能确定的,那么就无法确定反射目标了。
- 类型推理+字符串分析+指针分析(论文链接,一二作是李樾、谭添)。这个思路是从反射对象的使用点(usage points)开始反推。值得一提的是,2019年,两位老师又发表了新的研究成果。
- 动态分析辅助的静态分析(论文链接)。这个不必多言,就是从动态分析中获取信息来辅助进行静态分析,它会有动态分析的优点,但是也因此引入了动态分析的缺点。
Java native code难于分析的原因则是跨语言——最终会调用到C语言动态链接库中的代码。当前的一个解决思路是对关键的native code进行手动建模(用Java实现)。这里附上2020年的一个研究进展。
总结与思考
终于听完了所有视频课程。十分荣幸,收获颇多。再次感谢李樾、谭添两位老师的付出和分享!